使用Python完成一个完整的KNN算法
本篇文章使用python模拟实现一个简单的KNN算法,并且引入一些机器学习的基本概念。
1、数据准备
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import font_manager
% matplotlib inline
# raw_data_x是特征,raw_data_y是标签,0为良性,1为恶性
raw_data_X = [[3.393533211, 2.331273381],
[3.110073483, 1.781539638],
[1.343853454, 3.368312451],
[3.582294121, 4.679917921],
[2.280362211, 2.866990212],
[7.423436752, 4.685324231],
[5.745231231, 3.532131321],
[9.172112222, 2.511113104],
[7.927841231, 3.421455345],
[7.939831414, 0.791631213]
]
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]2、设置训练组
# 设置训练组
X_train = np.array(raw_data_X)
y_train = np.array(raw_data_y)
print(X_train.shape)
print(y_train.shape)
# print(y_train.flatten())
my_font = font_manager.FontProperties(fname='C:/Windows/Fonts/simsun.ttc',size=10)
# 将数据可视化
plt.scatter(X_train[y_train==0,0],X_train[y_train==0,1], color='g', label = '良性')
plt.scatter(X_train[y_train==1,0],X_train[y_train==1,1], color='r', label = '恶性')
plt.scatter(8.90933607318,3.365731514, color='b')
plt.xlabel('Tumor Size')
plt.ylabel('Time')
plt.annotate("target",
xy=(8.90933607318,3.365731514), xycoords='data',
xytext=(7,4), textcoords='data',
arrowprops=dict(arrowstyle="->",
connectionstyle="arc3"),
)
plt.legend(loc ="best",prop=my_font)
plt.axis([0,10,0,5])
plt.show()(10, 2)
(10,)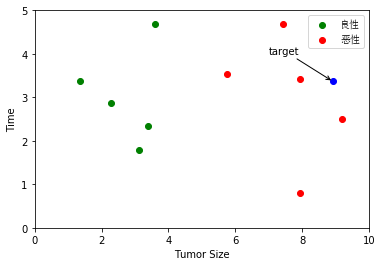
3、分类
那么现在给出一个肿瘤患者的数据(样本点)x:[8.90933607318, 3.365731514],是良性肿瘤还是恶性肿瘤
3.1、求距离
我们要做的是:求点x到数据集中每个点的距离,首先计算距离,使用欧氏距离
from math import sqrt
x=[8.90933607318, 3.365731514]
distances = [] # 用来记录x到样本数据集中每个点的距离
for x_train in X_train:
d = sqrt(np.sum((x_train - x) ** 2))
distances.append(d)
# 使用列表生成器,一行就能搞定,对于X_train中的每一个元素x_train都进行前面的运算,
# 把结果生成一个列表
distances = [sqrt(np.sum((x_train - x) ** 2)) for x_train in X_train]
distances
输出:
[5.611968000921151,
6.011747706769277,
7.565483059418645,
5.486753308891268,
6.647709180746875,
1.9872648870854204,
3.168477291709152,
0.8941051007010301,
0.9830754144862234,
2.7506238644678445]3.2、对距离排序
在求出距离列表之后,我们要找到最小的距离,需要进行一次排序操作。其实不是简单的排序,因为我们把只将距离排大小是没有意义的,我们要知道距离最小的k个点是在样本集中的位置。
这里我们使用函数:np.argsort(array) 对一个数组进行排序,返回的是相应的排序后结果的索引
nearest = np.argsort(distances)
nearest[0:6]输出:
array([7, 8, 5, 9, 6, 3], dtype=int64)然后我们选择k值,这里暂定为6,那就找出最近的6个点(top 6),并记录他们的标签值(y)
k = 6
topK_y = [y_train[i] for i in nearest[:k]]
topK_y输出:
[1, 1, 1, 1, 1, 0]3.3、决策规则
下面进入投票环节。找到与测试样本点最近的6个训练样本点的标签y是什么。可以查不同类别的点有多少个。
将数组中的元素和元素出现的频次进行统计
from collections import Counter
votes = Counter(topK_y)
votes输出:
Counter({1: 5, 0: 1})# Counter.most_common(n)
# 找出票数最多的n个元素,返回的是一个列表,
# 列表中的每个元素是一个元组,元组中第一个元素是对应的元素是谁
predict_y = votes.most_common(1)[0][0]
predict_y输出:1%%writefile kNN.py
import numpy as np
import math as sqrt
from collections import Counter
class kNNClassifier:
def __init__(self, k):
"""初始化分类器"""
assert k >= 1, "k must be valid"
self.k = k
self._X_train = None
self._y_train = None
def fit(self, X_train, y_train):
"""根据训练数据集X_train和y_train训练kNN分类器"""
assert X_train.shape[0] == y_train.shape[0], "the size of X_train must be equal to the size of y_train"
assert self.k <= X_train.shape[0], "the size of X_train must be at least k"
self._X_train = X_train
self._y_train = y_train
return self
def predict(self,X_predict):
"""给定待预测数据集X_predict,返回表示X_predict结果的向量"""
assert self._X_train is not None and self._y_train is not None, "must fit before predict!"
assert X_predict.shape[1] == self._X_train.shape[1], "the feature number of X_predict must be equal to X_train"
y_predict = [self._predict(x) for x in X_predict]
return np.array(y_predict)
def _predict(self, x):
distances = [sqrt.sqrt(np.sum((x_train - x) ** 2)) for x_train in self._X_train]
nearest = np.argsort(distances)
topK_y = [self._y_train[i] for i in nearest]
votes = Counter(topK_y)
return votes.most_common(1)[0][0]
def __repr__(self):
return "kNN(k=%d)" % self.k%run kNN.py
knn_clf = kNNClassifier(k=6)
knn_clf.fit(X_train, y_train)
x=np.array([[8.90933607318, 3.365731514]])
# print(x.reshape(1,-1))
X_predict = x.reshape(1,-1)
y_predict = knn_clf.predict(X_predict)
y_predict[0]输出:14、在sklearn中使用KNN
对于机器学习来说,其流程是:训练数据集 -> 机器学习算法 -fit-> 模型 输入样例 -> 模型 -predict-> 输出结果
我们之前说过,kNN算法没有模型,模型其实就是训练数据集,predict的过程就是求k近邻的过程。
我们使用sklearn中已经封装好的kNN库。你可以看到使用有多么简单。
from sklearn.neighbors import KNeighborsClassifier
# 创建kNN_classifier实例
kNN_classifier = KNeighborsClassifier(n_neighbors=6)
# kNN_classifier做一遍fit(拟合)的过程,没有返回值,
# 模型就存储在kNN_classifier实例中
a = kNN_classifier.fit(X_train, y_train)
print(a)
# kNN进行预测predict,需要传入一个矩阵,而不能是一个数组。reshape()成一个二维数组,第一个参数是1表示只有一个数据,第二个参数-1,numpy自动决定第二维度有多少
y_predict = a.predict(x.reshape(1,-1))
y_predictKNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=6, p=2,
weights='uniform')
array([1])在kNN_classifier.fit(X_train, y_train)这行代码后其实会有一个输出:
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=6, p=2,
weights='uniform')KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=6, p=2,
weights='uniform')参数:
class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, weights=’uniform’, algorithm=’auto’, leaf_size=30, p=2, metric=’minkowski’, metric_params=None, n_jobs=None, **kwargs)
我们研究一下参数:
n_neighbors: int, 可选参数(默认为 5)。用于kneighbors查询的默认邻居的数量weights(权重): str or callable(自定义类型), 可选参数(默认为 ‘uniform’)。用于预测的权重参数,可选参数如下:uniform: 统一的权重. 在每一个邻居区域里的点的权重都是一样的。distance: 权重点等于他们距离的倒数。使用此函数,更近的邻居对于所预测的点的影响更大。
[callable]: 一个用户自定义的方法,此方法接收一个距离的数组,然后返回一个相同形状并且包含权重的数组。
algorithm(算法): {‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, 可选参数(默认为 ‘auto’)。计算最近邻居用的算法:
ball_tree使用算法BallTreekd_tree使用算法KDTreebrute使用暴力搜索auto会基于传入fit方法的内容,选择最合适的算法。
注意 : 如果传入fit方法的输入是稀疏的,将会重载参数设置,直接使用暴力搜索。
leaf_size(叶子数量): int, 可选参数(默认为 30)。传入BallTree或者KDTree算法的叶子数量。此参数会影响构建、查询BallTree或者KDTree的速度,以及存储BallTree或者KDTree所需要的内存大小。此可选参数根据是否是问题所需选择性使用。p: integer, 可选参数(默认为 2)。用于Minkowski metric(闵可夫斯基空间)的超参数。p = 1, 相当于使用曼哈顿距离,p = 2, 相当于使用欧几里得距离],对于任何 p ,使用的是闵可夫斯基空间。metric(矩阵): string or callable, 默认为 ‘minkowski’。用于树的距离矩阵。默认为闵可夫斯基空间,如果和p=2一块使用相当于使用标准欧几里得矩阵. 所有可用的矩阵列表请查询 DistanceMetric 的文档。metric_params(矩阵参数): dict, 可选参数(默认为 None)。给矩阵方法使用的其他的关键词参数。n_jobs: int, 可选参数(默认为 1)。用于搜索邻居的,可并行运行的任务数量。如果为-1, 任务数量设置为CPU核的数量。不会影响fit
对于KNeighborsClassifier的方法:
| 方法名 | 含义 |
|---|---|
| fit(X, y) | 使用X作为训练数据,y作为目标值(类似于标签)来拟合模型。 |
| get_params([deep]) | 获取估值器的参数。 |
| neighbors([X, n_neighbors, return_distance]) | 查找一个或几个点的K个邻居。 |
| kneighbors_graph([X, n_neighbors, mode]) | 计算在X数组中每个点的k邻居的(权重)图。 |
| predict(X) | 给提供的数据预测对应的标签。 |
| predict_proba(X) | 返回测试数据X的概率估值 |
| score(X, y[, sample_weight]) | 返回给定测试数据和标签的平均准确值。 |
| set_params(**params) | 设置估值器的参数。 |
5、超参数
5.1、超参数简介
之前我们都是为knn算法传一个默认的k值。在具体使用时应该传递什么值合适呢?
这就涉及了机器学习领域中的一个重要问题:超参数。所谓超参数,就是在机器学习算法模型执行之前需要指定的参数。(调参调的就是超参数) 如kNN算法中的k。
与之相对的概念是模型参数,即算法过程中学习的属于这个模型的参数(kNN中没有模型参数,回归算法有很多模型参数)
如何选择最佳的超参数,这是机器学习中的一个永恒的问题。在实际业务场景中,调参的难度大很多,一般我们会业务领域知识、经验数值、实验搜索等方面获得最佳参数。### 4、在sklearn中使用KNN
5.2、寻找最好的k
5.2.1、对K进行遍历
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
import pandas as pd
iris = datasets.load_iris()
X = iris.data
y = iris.target
def train_test_split_temp(X, y, test_ratio=0.2, seed=None):
"""将矩阵X和标签y按照test_ration分割成X_train, X_test, y_train, y_test"""
assert X.shape[0] == y.shape[0], "the size of X must be equal to the size of y"
assert 0.0 <= test_ratio <= 1.0, "test_train must be valid"
if seed: # 是否使用随机种子,使随机结果相同,方便debug
np.random.seed(seed) # permutation(n) 可直接生成一个随机排列的数组,含有n个元素
shuffle_index = np.random.permutation(len(X))
test_size = int(len(X) * test_ratio)
test_index = shuffle_index[:test_size]
train_index = shuffle_index[test_size:]
X_train = X[train_index]
X_test = X[test_index]
y_train = y[train_index]
y_test = y[test_index]
return X_train, X_test, y_train, y_test
X_train1, X_test1, y_train1, y_test1 = train_test_split_temp(X, y)
# 指定最佳值的分数,初始化为0.0;设置最佳值k,初始值为-1
best_score = 0.0
best_k = -1
for k in range(1, 11): # 暂且设定到1~11的范围内
knn_clf = KNeighborsClassifier(n_neighbors=k)
knn_clf.fit(X_train1, y_train1)
score = knn_clf.score(X_test1, y_test1)
if score > best_score:
best_k = k
best_score = score
print("best_k = ", best_k)
print("best_score = ", best_score)输出:
best_k = 3
best_score = 0.9666666666666667可以看到,最好的k值是3,在我们设定的k的取值范围中间。需要注意的是,如果我们得到的值正好在边界上,我们需要稍微扩展一下取值范围。因为嘛,你懂的!
5.2.2、K折交叉验证
常用的交叉验证技术叫做K折交叉验证(K-fold Cross Validation)。 我们先把训练数据再分成训练集和验证集,之后使用训练集来训练模型,然后再验证集上评估模型的准确率。举个例子,比如一个模型有个参数叫$\alpha$,我们一开始不清楚要选择0.1还是1,所以这时候我们进行了交叉验证:把所有训练集分成K块,依次对每一个$\alpha$值评估它的准确率。
一般情况下数据量较少的时候我们取的K值会更大,为什么呢? 因为数据量较少的时候如果每次留出比较多的验证数据,对于训练模型本身来说是比较吃亏的,所以这时候我们尽可能使用更多的数据来训练模型。由于每次选择的验证数据量较少,这时候K折中的K值也会随之而增大,但到最后可以发现,无论K值如何选择,用来验证的样本个数都是等于总样本个数。
最极端的情况下,我们可以采用leave_one_out交叉验证,也就是每次只把一个样本当做验证数据,剩下的其他数据都当做是训练样本。
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import KFold
iris = datasets.load_iris()
X = iris.data
y = iris.target
# 定义我们想要搜索的K值
ks = range(1,11)
# 进行5折交叉验证,KFold返回的是每一折中训练数据和验证数据的index
# 假设数据样本为: [1,3,5,6,11,12,43,12,44,2], 总共10个样本
# 则返回的kf的格式为(前面的是训练数据,后面的是验证集):
# [0,1,3,5,6,7,8,9], [2,4]
# [0,1,2,4,6,7,8,9], [3,5]
# [1,2,3,4,5,6,7,8], [0,9]
# [0,1,2,3,4,5,7,9], [6,8]
# [0,2,3,4,5,6,8,9], [1,7]
kf = KFold(n_splits=5, random_state=1234, shuffle=True)
# 保存当前最好的K值和对应的准确率值
best_k = ks[0]
best_score = 0.0
# 循环每一个K值
for k in ks:
cur_score = 0
for train_index, valid_index in kf.split(X):
# print(train_index)
# 每一折的训练以及计算准确率
clf = KNeighborsClassifier(n_neighbors=k)
clf.fit(X[train_index], y[train_index])
cur_score = cur_score + clf.score(X[valid_index], y[valid_index])
# 求一下5折的平均准确率
avg_score = cur_score/5
if avg_score > best_score:
best_score = avg_score
best_k = k
print("current best score is %f"%best_score,"best k is %d"%best_k)
print("after cross validation, the final besk k is %d"%best_k)
输出:
current best score is 0.960000 best k is 1
current best score is 0.973333 best k is 8
current best score is 0.986667 best k is 9
after cross validation, the final besk k is 9sklearn中实现
#调用网格搜索方法
from sklearn.model_selection import GridSearchCV
param_search = {
"n_neighbors":[i for i in range(1,11)]
}
knn_clf = KNeighborsClassifier()
clf = GridSearchCV(knn_clf, param_search, cv=5)
clf.fit(X, y)
print("best score is %f"%clf.best_score_,"best k is ", clf.best_params_)输出:
best score is 0.980000 best k is {'n_neighbors': 6}对于交叉验证,决不能用测试数据来引导模型的训练
5.3、另一个超参数:权重
在回顾kNN算法思想时,我们应该还记得,对于简单的kNN算法,只需要考虑最近的n个数据是什么即可。但是如果我们考虑距离呢?
如果我们认为,距离样本数据点最近的节点,对其影响最大,那么我们使用距离的倒数作为权重。假设距离样本点最近的三个节点分别是红色、蓝色、蓝色,距离分别是1、4、3。那么普通的k近邻算法:蓝色获胜。考虑权重(距离的倒数):红色:1,蓝色:1/3 + 1/4 = 7/12,红色胜。
在 sklearn.neighbors 的构造函数 KNeighborsClassifier 中有一个参数:weights,默认是uniform即不考虑距离,也可以写distance来考虑距离权重(默认是欧拉距离,如果要是曼哈顿距离,则可以写参数p(明可夫斯基距离的参数),这个也是超参数)
因为有两个超参数,因此使用双重循环,去查找最合适的两个参数,并打印。
# 两种方式进行比较
best_method = ""
best_score = 0.0
best_k = -1
for method in ["uniform","distance"]:
for k in range(1, 11):
knn_clf = KNeighborsClassifier(n_neighbors=k, weights=method, p=2)
knn_clf.fit(X_train1, y_train1)
score = knn_clf.score(X_test1, y_test1)
if score > best_score:
best_k = k
best_score = score
best_method = method
print("best_method = ", method)
print("best_k = ", best_k)
print("best_score = ", best_score)
输出:
best_method = distance
best_k = 3
best_score = 0.96666666666666675.4、超参数网格搜索
在具体的超参数搜索过程中会需要很多问题,超参数过多、超参数之间相互依赖等等。如何一次性地把我们想要得到最好的超参数组合列出来。sklearn中专门封装了一个超参数网格搜索方法Grid Serach。
在进行网格搜索之前,首先需要定义一个搜索的参数param_search。是一个数组,数组中的每个元素是个字典,字典中的是对应的一组网格搜索,每一组网格搜索是这一组网格搜索每个参数的取值范围。键是参数的名称,值是键所对应的参数的列表。
param_search = [
{
"weights":["uniform"],
"n_neighbors":[i for i in range(1,11)]
},
{
"weights":["distance"],
"n_neighbors":[i for i in range(1,11)],
"p":[i for i in range(1,6)]
}
]可以看到,当weights = uniform即不使用距离时,我们只搜索超参数k,当weights = distance即使用距离时,需要看超参数p使用那个距离公式。下面创建要进行网格搜索所对应的分类算法并调用刚哥搜索:
knn_clf = KNeighborsClassifier()
#调用网格搜索方法
from sklearn.model_selection import GridSearchCV
# 定义网格搜索的对象grid_search,
# 其构造函数的第一个参数表示对哪一个分类器进行算法搜索,
# 第二个参数表示网格搜索相应的参数
grid_search = GridSearchCV(knn_clf, param_search)
下面就是针对X_train1, y_train1,使用grid_search在param_search列表中寻找最佳超参数组:
%%time
grid_search.fit(X_train1, y_train1)输出:
Wall time: 662 ms
GridSearchCV(cv=None, error_score='raise',
estimator=KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=5, p=2,
weights='uniform'),
fit_params=None, iid=True, n_jobs=1,
param_grid=[{'weights': ['uniform'], 'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]}, {'weights': ['distance'], 'n_neighbors': [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], 'p': [1, 2, 3, 4, 5]}],
pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
scoring=None, verbose=0)可以使用网格搜索的评估函数来返回最佳分类起所对应的参数
# 返回的是网格搜索搜索到的最佳的分类器对应的参数
grid_search.best_estimator_KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=5, p=2,
weights='uniform')也可以查看最佳参数的分类器的准确度。
我们会注意到,best_estimator_和best_score_参数后面有一个_。这是一种常见的语法规范,不是用户传入的参数,而是根据用户传入的规则,自己计算出来的结果,参数名字后面接_
grid_search.best_score_输出:
0.9833333333333333


